Levels of Understanding

There are different levels of understanding. While there are some concepts that a student may not understand, there are still connections that students make to previously learned material and concepts which serve to inform a recently learned procedure—and ultimately may lead to further understanding. In freshman calculus, for example, students learn an intuitive definition of limits and continuity which then allows them to learn the powerful applications of same; i.e. taking derivatives and finding integrals. It isn’t until they take more advanced courses (e.g., real analysis) that they learn the formal definition of limits and continuity and accompanying theorems. Does this mean that they don’t understand calculus?

Going to more basic mathematics, let’s look at multiplication. Learning multiplication—what it is and how to operate with it, provides an example of various levels of understanding. Efrat Furst, a cognitive neuroscientist who designs and teaches research-based classroom-oriented curriculum for educators and students addresses this. She writes:

Memorization usually means the ability to recite a certain fact like “four times three equals twelve” – a student that is able to do that is not considered to demonstrate understanding of multiplication. However, the student does understand “four times three” in a basic level that would allow effective communication at a low level and in a very specific context (i.e. answering a question in a math quiz). To create a higher level of understanding additional concrete examples are required (e.g. “Jess has three baskets, four balls in each”) as well as explicit connection to the new concept (“so we can say Jess has four balls multiplied by three”). By adding more familiar (concrete) examples that demonstrate the meaning of the concept we can establish a higher level of meaning for the concept “Multiplication”.

In other words, one can operate at a very basic level of understanding that grows over time. While some basic levels are thought of as “rote memorization”, lower level procedural skills inform higher level understanding skills in tandem. Reform math ignores this relationship and assumes that if a student cannot explain in writing a process used to solve a problem, that the student lacks understanding. Testing students for understanding in this manner, particularly in the K-8 grades, will often end up with students parroting explanations that they believe the teacher wants to hear—thus demonstrating a “rote understanding”.

How is understanding best measured, then? I maintain that understanding is not tested by words, but by whether the student has the mathematical tools and the skills to use them to solve problems.  At the K-12 levels, understanding is best measured by the proxies of procedural fluency and factual mastery. The mastery serves as evidence that higher skills grow out of lower ones.  I expect that this last statement will raise hackles on those who work within the educationist domain and try to build into their studies a confirmation that higher order thinking is at odds with lower procedural skills, and that focusing on procedures prevents understanding.

One proxy that teachers use for understanding and transfer of knowledge, is how well students can do all sorts of problem variations. A student in my seventh grade math class recently provided an example of this. As an intro to a lesson on complex fractions, I announced that at the end of the lesson they would be able to do the following problem:

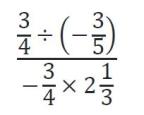
The boy raised his hand and said “Oh, I know how to solve that.” I recognized this as a “teaching moment” and said “OK, go for it”.  He narrated what needed to be done: “You divide the two fractions on top, by flipping the second one and multiplying, and since one is negative you’ll get a negative answer. You get -5/4.  Then you do the bottom, and you have to convert  to a fraction by multiplying 2 by 3 and adding 1, so you get 7/3 , and you multiply and you cross cancel and get -7/4 .”  Now you divide  by -7/4  so you flip the -7/4  and multiply. You have two negatives so your answer is positive. And you can cross cancel. You get 5/7.”

He had certainly never seen this exact same problem before. And while he did not know why the invert and multiply rule worked, nor could he explain why multiplying two negatives yield a positive product, he was able to orally dictate the method, taking it apart mentally and explaining it verbally. He put together basic skills that he learned and saw how they fit together and solved a more complex problem—which is what transference is about.

Problem Solving

Does understanding ever actually help in solving problems? In my experience, it does when the concept is part and parcel to the procedure. An example: knowing what procedure to use to simplify a² × a³ versus (a²)³ .  Students often have trouble remembering in which case exponents are added and in which one they are multiplied. The concept of multiplying powers is helpful; in the first case, the student remembers it is (a ×a) × (a × a × a), and it is easily seen that the exponents are added.  In the second case, raising a power to a power, the same principle applies: a² ×a² ×a²   , which lends itself to understanding that the exponent “2” is multiplied by 3. When the concept or derivation is not as closely attached, understanding the derivation does not provide an obvious benefit, such as certain trigonometric identities.

Likewise, in solving word problems, worked examples provide students a direct access to solving problems that are similar, and in the same category.  By scaffolding such problems;, that is varying the problems slightly beyond the initial worked example, students then are forced to stretch and to make connections that aren’t as obvious.

For example, students may be shown how to solve this type of problem: Two trains, 360 miles apart, head toward each other, one going at 100 mph and the other at 80 mph.  How long will it take them to meet?  The student can be shown that the sum of the two distances represented by 100t and 80t, where t is the time traveled by each train makes up the initial 360 miles.  A variation of this problem is: After the trains pass each other, how long will it take for them to be 90 miles apart?  In this case, the same concept is at work: the sum of the two distances represented by 100t and 80t, again where t is the time traveled by each train, makes up the future distance of 90 miles.

In the words of Dylan Wiliam (Emeritus Professor of Educational Assessment at the University College of London Institute of Education): “For novices, worked examples are more helpful than problem-solving even if your goal is problem-solving”

While people may criticize this as mere imitation, it is not.  As anyone knows who has learned a skill through initial imitation of specific techniques, such as drawing, bowling, swimming, dancing and the like, watching something and doing it are two different things. What looks like it will be easy often is more challenging than it appears. So too with math.

A frequent criticism of word problems in textbooks is that they present a worked example/method for solving a particular type of problem, followed by a set of almost identical problems to solve. Students may experience the practice of applying a memorized technique and mechanically look for the data to plug in to the appropriate equations without having to read the problem. But what if you are given values with different units in a distance/rate problem? And what if you are given two legs and
two different rates and need to find your average rate? Word problems can and should be varied for improving problem-solving ability. This is, in fact, what is done in well-written algebra textbooks or in problem sets devised by teachers. Students are given instruction via worked examples and some initial practice problems. After that, the problems vary.

 Ending the Fetish Over Understanding

The belief that teaching procedures prior to understanding will result in “math zombies” has become entrenched in educational culture. The people pushing these ideas view the world through an adult lens which they’ve acquired through the very practices that they feel do not work. They become angry that their teachers (supposedly) didn’t explain all these things to them and are certain that they would have liked math more and done better if only their teachers would have focused on understanding. Their views and philosophies are taken as faith by school administrations, school districts and many teachers — teachers who have been indoctrinated in schools of education that teach these methods.

The reform movement has succeeded in foisting its beliefs upon ever growing populations of new teachers who believe this is the only way. It is so entrenched, that even teachers who adamantly oppose such views feel guilty when teaching in the traditional manner so reviled by well-intentioned reformers. Given that today’s employers are complaining over the lack of basic math skills their recent college graduate employees possess, the math reform movement has created a poster child in which “understanding” foundational math is often not even “doing” math.